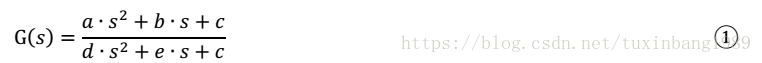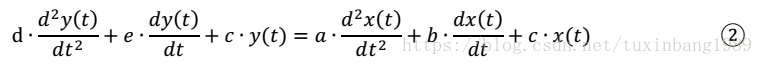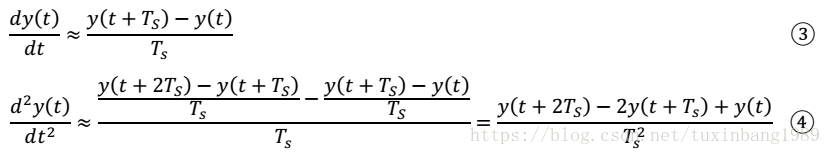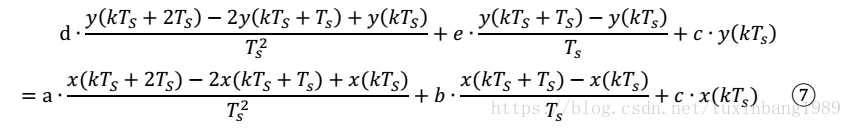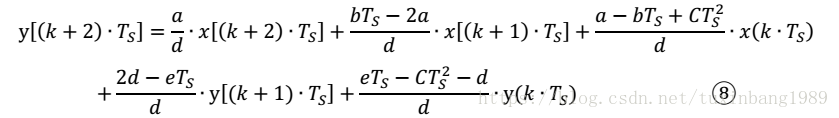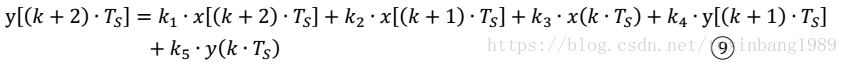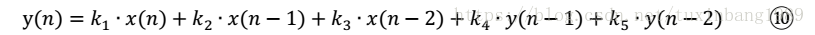滤波器的作用是允许某些频率的正弦信号基本无衰减的通过（增益为 1，频域 0dB），同时对另外某些频率的正弦信号起到衰减作用（增益在 0.707 以下，频域-3dB 以下）。 当然，滤波器对通过的正弦信号会产生一定的相移作用。

1.二阶通用滤波器

二阶滤波器表示的是滤波器时域表达式中最高含有二阶微分，或者说传递函数分母的s最高次数为2。滤波器对直流分量的增益为1。据此可设零状态二阶通用滤波器的传递函数为

时域表达式为

待定参数为a，b，c，d，e。

y(t)——输出信号，x(t)——输入信号。

现要将时域微分方程转换成对应离散域差分方程，假设采样周期为Ts。

根据微分的定义，有

由以上分析可知，Ts越小时，上述约等式越精确。

将连续量t分段，令t=kTs，k=0,1,2⋯，则微分方程可化为近似离散形式

将上述表达式代入到时域微分方程中，当Ts足够小时，近似认为

整理后得

进一步简化得

k1 ⋯ k5对应式⑧相应的系数，且满足

略去 Ts， 将时域离散信号转变成序列信号， 成为计算机能够运算的式子：

根据式⑩， 可以很容易写出二阶通用滤波器的运算程序。

2.二阶派生出的特殊滤波器

通过配置二阶通用滤波器的系数 a， b， c， d， e，可以生成多种特殊用途的滤波器：

根据所需滤波器的指标（截止频率、通带频率、阻带频率等）， 可以求出其传递函数的系数， 进一步推出通用型中的参数 abcde，再结合采样周期 Ts， 则可以算出数字滤波器的系数 k1/k2/k3/k4。

对于更高阶的滤波器， 可以根据要求， 对二阶滤波器进行串联组合（有些电机驱动器程序就是如此处理）。 例如， 要求一个高阶滤波器中含有低通环节、 带阻环节和超前滞后环节， 则可以先构造三个对应的二阶滤波器， 然后在运算中进行串行运算。

以上内容说明了对于二阶滤波器， 如何从模拟滤波器模型推出数字滤波器的计算程序。 对于整体的高阶滤波器（即非二阶组合型），上述方法过于繁琐，计算量大，则需要采用数字滤波中 IIR 和 FIR 滤波器设计方法，计算各差分量的系数， 请参考《信号与系统》教材。 建议采用 Matlab 中的 FDATOOL 进行滤波器设计， 直接生成 z 域系统方程的参数，非常方便。

参考程序：

typedef struct SecOrdFilter{float k1;float k2;float k3;float k4;float k5;float xin;float x1;float x2;float yout;float y1;float y2;} vector;#define SecondOrderFilter(v)    \                   // 后面将vector赋值给vyout = v.k1*v.xin + v.k2*v.x1+v.k3*v.x2+ v.k4*v.y1 + v.k5*v.y2;  \v.x2 = v.x1;     \v.x1 = v.xin;    \v.y2 = v.y1;     \v.y1 = v.yout;